5. Fashion Cycle â€哩s Illustrated in the Figure Above Represents:

A boundary layer is a thin layer of viscid fluid close to the solid surface of a wall in contact with a moving stream in which (inside its thickness δ) the menses velocity varies from zero at the wall (where the flow "sticks" to the wall considering of its viscosity) upward to U_e at the boundary, which approximately (within ane% error) corresponds to the free stream velocity (see Figure 1). Strictly speaking, the value of δ is an arbitrary value considering the friction force, depending on the molecular interaction between fluid and the solid trunk, decreases with the distance from the wall and becomes equal to zero at infinity.

Growth of a boundary layer on a flat plate.

Effigy 1. Growth of a purlieus layer on a flat plate.

The fundamental concept of the boundary layer was suggested past 50. Prandtl (1904), it defines the boundary layer as a layer of fluid developing in flows with very high Reynolds Numbers Re, that is with relatively low viscosity every bit compared with inertia forces. This is observed when bodies are exposed to loftier velocity air stream or when bodies are very large and the air stream velocity is moderate. In this instance, in a relatively thin boundary layer, friction Shear Stress (pasty shearing force): τ = η[∂u/∂y] (where η is the dynamic viscosity; u = u(y) – "contour" of the boundary layer longitudinal velocity component, see Figure ane) may be very large; in particular, at the wall where u = 0 and τ_w = η[∂u/∂y]_west although the viscosity itself may be rather modest.

It is possible to ignore friction forces outside the boundary layer (as compared with inertia forces), and on the ground of Prandtl's concept, to consider two flow regions: the purlieus layer where friction furnishings are large and the almost Inviscid Flow core. On the premises that the boundary layer is a very sparse layer (δ << Fifty, where L is the characteristic linear dimension of the torso over which the flow occurs or the channel containing the menses, its thickness decreasing with growth of Re, Effigy 1), i tin can estimate the lodge of magnitude of the boundary layer thickness from the following relationship:

(ane)

For instance, when an plane flies at U_e = 400 km/hr, the boundary layer thickness at the wing trailing edge with i meter chord (profile length) is m. As was experimentally established, a laminar boundary layer develops at the inlet department of the body. Gradually, under the influence of some destabilizing factors, the boundary layer becomes unstable and transition of boundary layer to a Turbulent Menstruum regime takes identify. Special experimental investigations accept established the existence of a transition region between the turbulent and laminar regions. In some cases (for example, at high turbulence level of the external menses), the boundary layer becomes turbulent immediately downstream of the stagnation point of the flow. Nether some conditions, such as a astringent pressure drop, an inverse phenomenon takes place in accelerating turbulent flows, namely period relaminarization.

In spite of its relative thinness, the boundary layer is very important for initiating processes of dynamic interaction between the flow and the body. The boundary layer determines the aerodynamic drag and lift of the flight vehicle, or the energy loss for fluid catamenia in channels (in this case, a hydrodynamic purlieus layer considering there is likewise a thermal boundary layer which determines the thermodynamic interaction of Estrus Transfer).

Computation of the boundary layer parameters is based on the solution of equations obtained from the Navier–Stokes equations for pasty fluid motion, which are get-go considerably simplified taking into business relationship the thinness of the purlieus layer.

The solution suggested by L. Prandtl is essentially the first term of power series expansion of the Navier–Stokes equation, the series expansion being performed for powers of dimensionless parameter (δ/50). The smaller parameter in this term is in zero power so that the boundary layer equation is the zip approximation in an Asymptotic Expansion (at large Re) of the boundary layer equation (asymptotic solution).

A transformation of the Navier–Stokes equation into the purlieus layer equations can be demonstrated by deriving the Prandtl equation for laminar boundary layer in a two-dimensional incompressible flow without trunk forces.

In this case, the arrangement of Navier–Stokes equations will be:

(2)

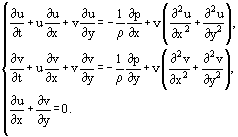
After evaluating the society of magnitude of some terms of Eq. (2) and ignoring small terms the system of Prandtl equations for laminar boundary layer becomes:

(iii)

in which x, y are longitudinal and lateral coordinates (Figure i); v is the velocity component along "y" axis; p, pressure; t, fourth dimension; and north the kinematic viscosity.

The boundary layer is thin and the velocity at its external edge U_e tin can be sufficiently and accurately determined as the velocity of an ideal (inviscid) fluid flow along the wall calculated up to the commencement approximation, without taking into account the reverse action of the boundary layer on the external flow. The longitudinal pressure gradient [∂p/∂x] = [dp/dx] (at p(y) = const ) in Eq. (3) can be depicted from the Euler equation of motion of an ideal fluid . From the above, Prandtl equations in their finite form will be written every bit:

(4)

This is a organization of parabolic, nonlinear partial differential equations of the 2nd social club which are solved with initial and boundary conditions

The system of equations (4) is written for actual values of velocity components u and 5. To generalize the equations obtained for turbulent flow, the well-known relationship between actual, averaged and pulsating components of turbulent flows parameters should be used. For example, for velocity components there are relationships connecting actual u and v, average ū and and pulsating u' and five' components:

After some rearrangements, it is possible to obtain another system of equations [Eq. (6)] from organization (3), in item for steady flow:

(half dozen)

Using the following relation for friction shear stress in the boundary layer:

(7)

and taking into account that in the laminar boundary layer u = u' and it is possible to rewrite the Prandtl equations in a form valid for both laminar and turbulent flows:

(viii)

The simplest solutions have been obtained for a laminar boundary layer on a sparse flat plate in a two-dimensional, parallel flow of incompressible fluid (Figure 1). In this instance, the estimation of the order of magnitude of the equations terms: x ~ Fifty, y ~ δ, δ ~ allows combining variables ten and y in one relation

(ix)

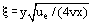
and to reduce the solution of Eq. (8) (at dp/dx = 0) to determining the dependencies of u and v upon the new parameter ξ. On the other hand, using well-known relations between velocity components u, v and stream office ψ

it is possible to obtain one ordinary nonlinear differential equation of the third guild, instead of the system of partial differential equations (8)

(10)

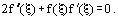
Here, f(ξ) is the unknown office of ξ variable: f = ƒ =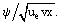

The beginning numerical solution of Eq. (ten) was obtained past Blasius (1908) nether boundary conditions corresponding to physical conditions of the boundary layer at y = 0: u = 0, v = 0; at y → ∞; u → U_e (Blasius boundary layer).

Figure 2 compares the results of Blasius solution (solid line) with experimental information. Using these data, information technology is possible to evaluate the viscous boundary layer thickness. At ξ 2.5, (u/U_e 0.99) (Figure ii); consequently from Eq. (9) we obtain:

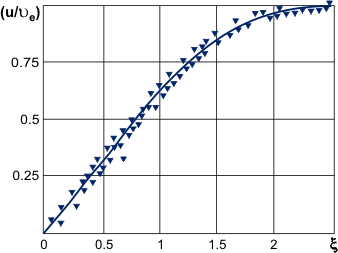
Figure 2.

From the Blasius numerical calculations of the value of the 2d derivative of f(ξ) function at the wall friction shear stress, the human relationship in this case is:

(11)

Friction force R, acting on both sides of the plate of L length (Figure 1), is likewise determined from Eq. (xi):

as in the friction coefficient for flat plates:

Despite the fact that Prandtl equations are much simpler than Navier–Stokes equations, their solutions were obtained for a express number of problems. For many applied problems, it is not necessary to determine velocity profiles in the boundary layer, only thickness and shear stress. This kind of information may be obtained by solving the integral momentum equation

(12)

The integral relationship (12) is valid both for the laminar and turbulent boundary layer.

Functions which were not known a priori only which characterize distribution of fluid parameters beyond the layer thickness δ are under the integral in Eq. (12). And the error of computing the integral is less than the error in the approximately assumed integrand function ρu = ρu(y). These create atmospheric condition for developing approximate methods of calculating boundary layer parameters which are less time-consuming than the verbal methods of integrating Prandtl equations. The cardinal concept was kickoff suggested by T. von Karman, who introduced such arbitrary layer thickness δ*

(13)

and momentum displacement thickness δ**

(14)

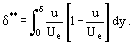
thus, we tin can transform Eq. (12) for two-dimensional boundary layer of incompressible fluid to:

(xv)

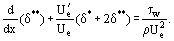
There are three unknown functions in Eq. (15), namely, δ* = δ*(x), δ** = δ**(ten) and τ_westward = τ_w(ten) [functions of U_east(10) and correspondingly which are known from computations of flow in the inviscid catamenia cadre].

The solution of an ordinary differential equation like Eq. (fifteen) unremarkably requires supposition (or representation) of velocity distribution (velocity profile) across the purlieus layer thickness as the role of some characteristic parameters (form-parameters), and information technology also requires the employ of empirical data about the relationship between friction coefficient C_f = 2τ_w/(ρU² _e) and the capricious thickness of the boundary layer (friction police force).

Some definite physical explanations can exist given as far equally the values of δ* and δ** are concerned. The integrand function in Eq. (13) contains afterwards rearrangement, a term (U_e – u) which characterizes the velocity decrease. The integral in Eq. (14) tin thus be considered equally a measure of decreasing the menstruum rate across the boundary layer, as compared with the perfect fluid flow at the velocity U_e. On the other paw, the value of δ* can be considered equally the measure of deviation along a normal to the wall (along "y" centrality) of the external menstruation stream line under the influence of friction forces. From this consideration of the integral construction of Eq. (14), it is possible to conclude that δ** characterizes momentum decrease in the boundary layer under the influence of friction.

The following relations are valid:

where H is the class-parameter of the boundary layer velocity contour. For example, for linear distribution u = ky,

At present, and then-called semi-empirical theories are widely used for predicting turbulent boundary layer parameters. In this case, it is causeless that total friction stress τ in a turbulent boundary layer is a sum

(16)

Hither, τ_T is additional (turbulent or Reynolds) friction stress, in item, in an incompressible flow see Eq. (7).

This representation is directly connected with the system of equations of movement in the boundary layer (6). In the compressible boundary layer, density pulsations tin can be considered to exist the outcome of temperature pulsations

(17)

where β = (ane/T) is the volumetric expansion coefficient.

Additional semi-empirical hypotheses about turbulent momentum transfer are used for determining τ_T. For example,

where η_T is the dynamic coefficient of turbulent viscosity introduced by J. Boussinesq in 1877.

On the ground of the concept of similarity of molecular and turbulent commutation ( similarity theory ) Prandtl introduced the mixing length (die Mischungsweg) hypothesis . The mixing length one is the path a finite fluid volume ("mole") passes from one layer of average motion to another without changing its momentum. In accordance with this status, he derived an equation which proved to be fundamental for the purlieus layer theory:

(18)

For turbulent region of the near wall flow boundary layer, L. Prandtl considered the length ane proportional to y

(19)

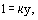
where κ is an empirical constant.

Close to the wall, where η_T << η, sticky molecular friction [the offset term in Eq. (15)] is a determining cistron. The thickness of this function of the purlieus layer δ₁, which is known as laminar or gummy sublayer, is . Outside the sublayer, the value of η_T increases, reaching several orders of magnitude larger than η. Correspondingly, in this zone of the boundary layer known as the turbulent core τ_T > ₀ = η[∂ū/∂y]. Sometimes the turbulent core is subdivided into the buffer zone, where the laminar and turbulent friction are the comparable value, and the developed zone, where τ_T >> τ₀. For this region, subsequently integrating Eq. (18) and taking into business relationship Eq. (xix), information technology is possible to derive an expression for logarithmic velocity profile :

(20)

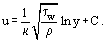
If dimensionless (or universal) coordinates are used.

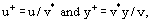
where is the then-called dynamic velocity (or Friction Velocity), Eq. (20) can be rewritten in the following form:

(21)

Velocity distribution representation in universal coordinates and mathematical models for turbulent viscosity coefficient are dealt with in greater detail in the department of Turbulent Menstruum.

One of the current versions of the semi-empirical theory of turbulent purlieus layer adult by S. S. Kutateladze and A. I. Leontiev is based on the and then-chosen asymptotic theory of turbulent boundary layers at Re → ∞ where the thickness of laminar (viscous) sublayer δ_one decreases at a higher rate than δ as a consequence of which (δ_one/δ) → 0.

Under these conditions, a turbulent purlieus layer with "vanishing viscosity" is developing. In this layer, η → 0 but is non equal to cypher and in this respect, the layer differs from perfect fluid flow. The concept of relative friction law, introduced past S. South. Kutateladze and A. I. Leontiev (1990), indicates

(22)

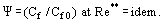
The law is defined equally the ratio of friction coefficient C_f for the condition under consideration to the value of C_f0 for "standard" conditions on a flat, impermeable plate flown effectually by incompressible, isothermal menstruum, both coefficients being obtained for Re** = U_eδ**/ν. It is shown that at Re → ∞; η → 0; and C_f → 0, the relative variation of the friction coefficient under the influence of such disturbing factors as _{pressure level gradient, compressibility}, nonisothermicity, injection (suction) through a porous wall etc., has a finite value.

The equations derived for calculating the value of Ψ accept one important characteristic which makes Ψ contained of empirical constants of turbulence. In accordance with the fundamental concept of the integral "approach", the integral momentum equation is transformed into:

(23)

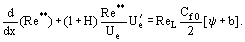
Hither, 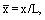Re₅₀ = U_eL/ν, b = (two/C_f0)(ρ_westwardU_w)/(ρ_eastU_e) are the permeability parameters for the case of injecting a gas at density ρ_w through a permeable wall at the velocity of v_w. For determining the office Re** = Re** , it is necessary to summate the distribution For this purpose, the principle of superposition of disturbing factors applies

(24)

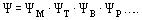
In Eq. 24, each multiplier represents the relative friction law, taking into business relationship the consequence of 1 of the factors, amongst them compressibility Ψ_M, temperature (or Enthalpy) head Ψ_T, injection Ψ_B, pressure gradient Ψ_P and others.

The cardinal concepts of the boundary layer create weather condition for explaining such phenomena as flow separation from the surface under the influence of the flow inertia, deceleration of viscous flow by the wall and adverse pressure level slope acting in the upstream direction [∂p/∂ten] = [dp/dx[ >] 0 or [∂u/x∂] < 0.

If pressure gradient is agin on the surface location between sections '1–iv' (see Figure 3), the velocity distribution u = u(10,y) in the boundary layer changes gradually; becoming "less total," decreasing the inclination in the fluid jets which are closer to the wall and possessing less amount of kinetic energy (see velocity profile shapes in Figure 3) which penetrate far downstream into the region of increased pressure. In some sections, for instance section '4', fluid particles which are on the 'a-a' stream line (dotted line in Figure 3) — having completely exhausted their supply of kinetic energy go decelerated (u_a = 0).

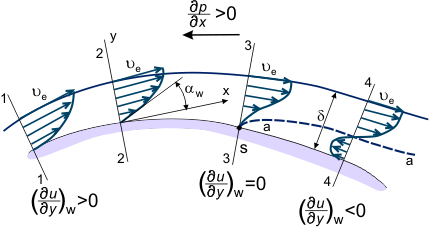
Boundary layer in flow over a covered surface.

Figure 3. Purlieus layer in flow over a covered surface.

Static pressure and pressure gradient value do non vary beyond boundary layer thickness. Therefore, fluid particles which are closer to the wall than line 'a–a' and possessing even so less amount of energy begin to motion in the opposite direction under the influence of the pressure gradient in '4–4' department (see Figure 3). Thus, the relationship:

In this way, at some locations of the surface, the velocity profile changes. This change is characterized by the alteration of the sign of the derivative [∂u/∂y]_westward from positive (department 2, Figure 3) to negative (section 4). Of course, it is also possible to define the section where [∂u/∂y]_w = 0 (section three, Figure 3). This is referred to as the purlieus layer separation department (correspondingly point 'S' on the surface of this section is the separation indicate). Information technology is characterized past the development of a reverse menstruation zone — the flow around the body is no longer polish, the boundary layer becomes considerably thicker and the external catamenia stream lines deviate from the surface of the trunk flown effectually. Downstream of the separation indicate, the static pressure distribution across the thickness of the layer is not steady and the static pressure distribution along the surface does not correspond to the pressure distribution in the external, inviscid flow.

The separation is followed by the development of reverse catamenia zones and swirls, in which the kinetic energy supplied from the external flow transforms into heat under the influence of friction forces. The flow separation, accompanied by energy dissipation in the reverse flow swirl zones, results in such undesirable effects as increases in the flying vehicles' drag or hydraulic losses in channels.

On the other hand, separated flows are used in different devices for intensive mixing of fluid (for example, to improve mixing of fuel and air in combustion chambers of engines). When viscous fluids flow in channels with a variable cross-section (alternating pressure gradient), the separation zone may be local if the diffusor section is followed by the confusor section, where the separated flow will again reattach to the surface (see Figure 4a). When the catamenia separates from the trailing border of the body (for case, from the fly trailing edge), the so-called wake is formed by "linking" boundary layers (see Figure 4b).

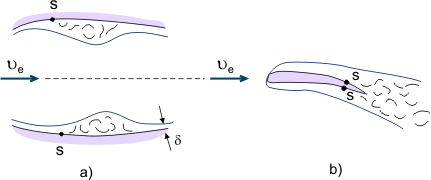
Boundary layer separation phenomena.

Figure iv. Boundary layer separation phenomena.

REFERENCES

Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung : Verhandl. III Int. Math. Kongr. — Heidelberg.

Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys. , 56:ane–37.

Kutateladze, S. S. and Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers , Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.